Методика расчета средней цены и доходности

По каким формулам рассчитывается доходность инвестиций?

Специфика расчета доходности инвестиционного портфеля во многом будет зависеть от того, как именно вы им управляете, какие сделки проводите и какие финансовые инструменты используете. Рассмотрим несколько наиболее частых ситуаций и расскажем, как считается доходность для каждой из них.

Для расчетов будем использовать несколько важных показателей:

Стоимость позиции — стоимость актива в портфеле.

Средняя цена — цена актива, от которой рассчитывается прибыль или убыток по позиции.

Абсолютная доходность — доходность позиции относительно ее средней цены в рублях, долларах США или евро.

Относительная доходность — доходность позиции относительно ее средней цены в процентах.

Ситуация 1. Купили актив, больше его не покупаете и не продаете

Представим, что вы просто купили интересующий вас актив, который не планируете продавать или докупать. В этом случае доходность позиции будет считаться как разница между ценой покупки и текущей ценой актива на бирже.

Например, вы купили 10 акций компании Х по цене 100 ₽. Через некоторое время цена на акции Х выросла до 150 ₽.

Абсолютная доходность = (количество акций × текущая биржевая цена) − (количество акций в момент покупки × цена акций в момент покупки), или (10 × 150) − (10 × 100) = 500 ₽.

Относительная доходность = (абсолютная доходность) / (количество акций × цена покупки) × 100%, или 500 / (10 × 100) × 100% = 50%

Ситуация 2. Периодически докупаете один и тот же актив, не продаете

Представим, что вы купили интересующий вас актив, которые не планируете продавать, только периодически докупать в разное время. В этом случае мы посчитаем среднюю цену покупки по методу среднего арифметического значения, а затем будем считать доходность позиции как разницу между средней ценой актива и текущей ценой актива на бирже.

Например, вы купили 10 акций компании Х по цене 100 ₽. Через некоторое время цена на акции Х выросла до 130 ₽, но вы решили купить еще 20 акций.

Средняя цена акций = ((цена первой покупки × количество акций) + (цена второй покупки × количество акций)) / (общее количество акций), или ((100 × 10) + (130 × 20)) / 30 = 120 ₽.

Еще через некоторое время цена акций выросла до 160 ₽.

Абсолютная доходность = (количество акций × текущая биржевая цена) − (общее количество акций × средняя цена), или (30 × 160) − (30 × 120) = 1200 ₽.

Относительная доходность = (абсолютная доходность) / (количество акций × средняя цена) × 100%, или 1200 / (30 × 120) × 100% = 33,33%.

Важно: для расчета средней цены покупки валюты действуют дополнительные правила. Дивиденды, купоны и любые другие поступления валюты учитываются как покупка валюты. Вывод валюты, покупка валютных ценных бумаг и комиссии, уменьшающие валютную позицию, учитываются как продажа валюты. Это необходимо для правильного учета средней цены.

Ситуация 3. Несколько раз купили один и тот же инструмент, потом часть продали

В этом случае расчеты будут выглядеть немного сложнее. Есть два варианта подсчета средней цены позиции, от которой затем считается доходность: по методу ФИФО или по методу средневзвешенной цены.

ФИФО (от английского First In First Out / FIFO) — это метод, по которому ведется учет активов на брокерских счетах и расчет налогооблагаемой базы с точки зрения налогового законодательства.

ФИФО применяется, когда один и тот же актив в портфеле — например, акции определенной компании — покупался в ходе нескольких сделок и по разным ценам. Тогда при продаже части позиции по этому активу первыми будут учитываться те акции, которые приобретались раньше всего. Отображение средней цены по ФИФО позволяет посмотреть, как будет выглядеть ваша база для расчета налога с точки зрения Налогового кодекса РФ.

Например, вы купили акции Х за три сделки. Сначала вы купили одну акцию по цене 30 ₽. Через неделю купили вторую акцию по цене 80 ₽, а через месяц купили еще одну по цене 100 ₽.

Средняя цена акций Х после трех покупок: (30 + 80 + 100) / 3 = 70 ₽.

Абсолютная доходность акций Х при текущей цене в 100 ₽: (количество акций × текущая биржевая цена) − (общее количество акций × средняя цена), или (3 × 100) − (3 × 70) = 90 ₽.

Относительная доходность акций Х при текущей цене в 100 ₽: (абсолютная доходность) / (количество акций × средняя цена) × 100%, или 90 / (3 × 70) × 100% = 42,85%.

Спустя два месяца цена на эти акции выросла до 150 ₽ за штуку, и вы решили продать две акции из вашего портфеля. Вот как будет выглядеть расчет средней цены по методу ФИФО:

Сначала из средней цены вычеркивается акция, которую вы купили первой по цене 30 ₽.

Затем вычитается акция, которую вы купили второй по цене 80 ₽.

В результате продажи в портфеле останется одна акция с ценой покупки по 100 ₽. Это и будет средняя цена, от которой будет считаться абсолютная и относительная доходность позиции.

Абсолютная доходность акции Х при текущей цене в 150 ₽: (количество акций × текущая биржевая цена) − (общее количество акций × средняя цена), или (1 × 150) − (1 × 100) = 50 ₽.

Относительная доходность акции Х при текущей цене в 150 ₽: (абсолютная доходность) / (количество акций × средняя цена) × 100%, или 50 / (1 × 100) × 100% = 50%.

Метод средневзвешенной цены — позволяет оценить эффективную доходность ваших открытых позиций: средняя цена актива изменяется только в том случае, если вы докупаете активы, и не изменяется, когда вы частично продаете их.

Например, вы сформировали в своем портфеле позицию по акциям компании Х и для этого совершили три сделки. Сначала вы купили одну акцию по цене 30 ₽. Через неделю купили вторую акцию по цене 80 ₽, а через месяц добавили еще одну, но уже по цене 100 ₽.

Средняя цена акции Х после трех покупок: (30 + 80 + 100) / 3 = 70 ₽.

Абсолютная доходность акций Х при текущей цене в 100 ₽: (количество акций × текущая биржевая цена) − (общее количество акций × средняя цена), или (3 × 100) − (3 × 70) = 90 ₽.

Относительная доходность акций Х при текущей цене в 100 ₽: (абсолютная доходность) / (количество акций × средняя цена) × 100%, или 90 / (3 × 70) × 100% = 42,85%.

Спустя два месяца цена на эти акции выросла до 120 ₽ за штуку, и вы решили продать две акции из вашего портфеля. Вы не обнулили позицию по акциям Х, поэтому их средняя цена не изменится и останется на средней цене в 70 ₽ за акцию.

Абсолютная доходность акции Х при текущей цене в 120 ₽: (количество акций × текущая биржевая цена) − (общее количество акций × средняя цена), или (1 × 120) − (1 × 70) = 50 ₽.

Относительная доходность акций Х при текущей цене в 120 ₽: (абсолютная доходность) / (количество акций × средняя цена) × 100%, или 50 / (1 × 70) × 100% = 71,43%.

Ситуация 4. Сделки с облигациями

Доходность по облигациям на вкладке «Портфель» не учитывает накопленный купонный доход (НКД) и выплаченный купонный доход.

Например, вы купили три облигации по цене 990 ₽. В момент покупки вы заплатили НКД в размере 10 ₽. Средняя цена облигаций будет равна цене покупки — 990 ₽. Спустя месяц цена облигаций выросла до 1000 ₽, НКД составляет 20 ₽.

Абсолютная доходность облигаций = (количество облигаций × текущая биржевая цена) − (количество облигаций × средняя цена), или (3 × 1000) − (3 × 990) = 30 ₽.

Относительная доходность облигаций = (абсолютная доходность) / (количество облигаций × средняя цена) × 100%, или 30 / (3 × 990) × 100% = 1,01%.

Если у облигации есть эффект амортизации, то при расчете средней цены и доходности амортизация будет учтена только после того, как номинал облигации зачислят на торговый счет.

Ситуация 5. Сделки с фьючерсами

В случае сделок с фьючерсами перед расчетом доходности стоимость фьючерса в пунктах приводится к рублям, даже если базовый актив фьючерса номинирован в валюте.

Например, у вас в портфеле есть 2 фьючерса на индекс РТС. Один из них вы купили по оценочной стоимости 182 110 пунктов, а второй докупили позже по стоимости 182 300 пунктов.

Сейчас фьючерс оценивается в 183 500 пунктов. Минимальный шаг цены — 10 пунктов. Стоимость шага цены — 20 ₽.

Чтобы рассчитать доходность фьючерсной позиции, нужно перевести оценочную стоимость фьючерса в рубли. Для этого найдем стоимость одного шага цены: (стоимость шага цены / минимальный шаг цены), или 20 / 10 = 2 ₽. При этом важно помнить, что шаг цены может меняться и при расчете доходности нужно использовать этот показатель на момент сделки.

Средняя цена фьючерсной позиции в пунктах: (оценочная стоимость фьючерса в пунктах) / (количество фьючерсов), или (182 110 + 182 300) / 2 = 182 205 пунктов.

Средняя цена фьючерсной позиции в рублях: ((стоимость первого фьючерса в пунктах × стоимость пункта на момент первой сделки) + (стоимость второго фьючерса в пунктах × стоимость пункта на момент второй сделки)) / (количество фьючерсов), или ((182 110 × 2) + (182 300 × 2)) / 2 = 364 410 ₽.

Текущая стоимость одного фьючерса на индекс РТС в рублях: (стоимость фьючерса в пунктах × стоимость пункта), или (183 500 × 2) = 367 000 ₽.

Абсолютная доходность фьючерсов в портфеле: (стоимость фьючерса в рублях − средняя цена в рублях) × (количество фьючерсов в портфеле), или (367 000 − 364 410) × 2 = 5180 ₽.

Относительная доходность фьючерсов в портфеле: (абсолютная доходность фьючерсов) / (средняя цена фьючерсной позиции в рублях) × 100%, или 5180 / 364 410 × 100% = 1,42%.

Что такое средняя цена и для чего она нужна?

Средняя цена акции — это значение, которое показывает среднюю цену, по которой вы сформировали позицию по ценной бумаге. Именно от средней цены рассчитывается прибыль или убыток по позиции.

Если вы купите акции за одну сделку, то средняя цена покупки будет такой же, как цена самой сделки, а доходность будет посчитать легко.

Например, вы купили 11 акций компании Х по 100 ₽. Затем они выросли до 120 ₽. Доходность составит: (120 − 100) × 11 = 220 ₽.

Но если вы купите актив за несколько сделок с разной ценой, то формула расчета доходности заметно усложнится: в ней придется использовать данные о каждой сделке.

Например, вы купили 5 акций Y по 54 ₽, затем еще 7 акций той же компании по 65 ₽ и еще 2 акции по 47 ₽. Спустя некоторое время стоимость акций выросла до 80 ₽.

Формула расчета доходности стала очень длинной: ((80 − 54) × 5) + ((80 − 65) × 7) + ((80 − 47) × 2) = 301 ₽.

Чем больше было сделок по разной цене, тем длиннее станет формула. Чтобы упростить расчет доходности, можно ввести понятие средней цены покупки акции.

Средняя цена покупки акций Y из прошлого примера: (54 × 5 + 65 × 7 + 47 × 2) / (5 + 7 + 2) = 58,5 ₽.

Теперь мы знаем среднюю цену, по которой сформировали свою позицию. Рассчитать доходность станет легче: (80 − 58,5) × (5 + 7 + 2) = 301 ₽.

Посмотреть среднюю цену акции или любого другого актива из вашего портфеля можно в приложении Тинькофф Инвестиций.

Средняя цена указывается на странице актива. Слева от стрелочки — средняя цена покупки, справа — текущая цена актива

EPS: что такое прибыль на одну акцию и что она дает инвестору

Один из главных показателей финансовой отчетности — это прибыль на акцию (EPS). Рассказываем, какие виды этого показателя бывают, как их рассчитать, где их можно найти в отчетности и как инвестор может их использовать

В этом тексте про EPS вы узнаете:

Что такое EPS

Аббревиатура EPS означает Earnings Per Share, что переводится как «прибыль на акцию».

EPS — это чистая прибыль компании, приходящаяся на ее каждую обыкновенную акцию, находящуюся в обращении.

EPS обычно используется инвесторами для оценки инвестиционной привлекательности компании, позволяя соотносить уровень прибыльности непосредственно со стоимостью одной акции. Поэтому EPS является широко используемой метрикой для оценки корпоративной стоимости.

Важно не путать EPS с дивидендами на одну акцию. Дивиденды — это сумма реально выплачиваемых на каждую акцию денег, а EPS — это сумма дохода компании, отображенного в отчетности и приходящегося на одну акцию.

Чем больше EPS, тем более ценной становится акция. Значение EPS зависит не только от размера прибыли, но и от количества акций. EPS может вырасти не только из-за роста прибыли, но и из-за уменьшения количества акций.

Какие есть виды EPS и как они рассчитываются

Инвесторы и аналитики используют несколько основных видов EPS:

• базовая;
• разводненная (Diluted);
• от продолжающейся деятельности;
• за вычетом чрезвычайных статей.

Базовая прибыль на одну акцию

Базовая EPS — это показатель, позволяющий увидеть, сколько прибыли компании, подлежащей распределению между владельцами обыкновенных акций, приходится на каждую обыкновенную акцию.

Базовая EPS рассчитывается по формуле:

Basic EPS = (NP — PD)/CSO,

NP — чистая прибыль компании,

PD — сумма дивидендов, выплачиваемая по привилегированным акциям,

CSO — количество обыкновенных акций компании, находящихся в обращении.

Компания в течение года может выпускать или выкупать акции. Из-за этого количество акций меняется. Более точно базовое EPS рассчитывается, если использовать средневзвешенное количество акций в обращении в течение периода. В качестве веса применяется количество дней, в течение которых обращалось соответствующее количество акций.

Например, у компании в обращении был 1 000 000 акций, но за 30 дней до окончания года было выпущено 200 000 новых обыкновенных акций. Можно EPS рассчитывать, исходя из количества акций на конец года — 1 200 000, а можно в расчете применить средневзвешенное количество акций — 1 000 000 х 335 + 1 200 000 х 30)/365 = 1 016 438.

В этом случае формула расчета будет такой:

Basic EPS = (NP — PD)/WACSO,

NP — чистая прибыль компании,

PD — сумма дивидендов, выплачиваемая по привилегированным акциям,

WACSO — средневзвешенное количество обыкновенных акций.

Обычно в финансовой отчетности компания указывает число акций, использованное для расчета EPS.

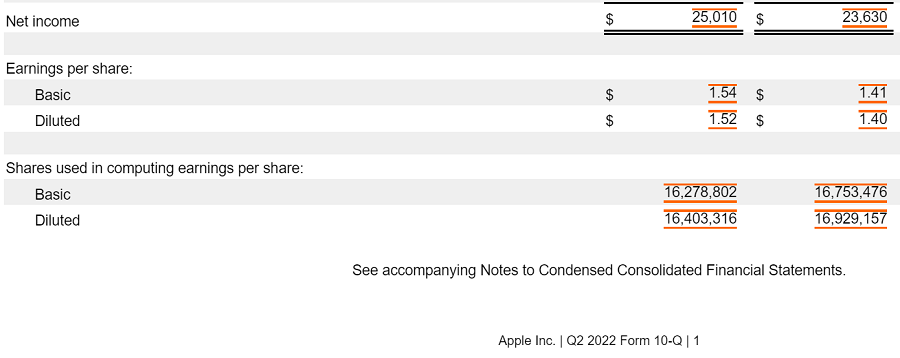
Прибыль на акцию и количество акций, используемое при расчете EPS в отчете о прибылях и убытках Apple

Разводненная EPS

Разводненная EPS (Diluted EPS) — это прибыль на одну обыкновенную акцию с учетом возможного появления новых акций и в случае исполнения различных условных соглашений — конвертации привилегированных акций или облигаций, исполнения опционов, варрантов и пр.

Разводненная EPS меньше базовой, поэтому инвесторы могут чаще ориентироваться именно на нее, то есть смотреть на показатель с более консервативных позиций.

Разводненная EPS рассчитывается по формуле:

Diluted EPS = (NP — PD)/ (WACSO + СDS),

NP — чистая прибыль компании,

PD — сумма дивидендов, выплачиваемая по привилегированным акциям,

WACSO — средневзвешенное количество обыкновенных акций, находящихся в обращении,

СDS — количество акций, которое может добавиться в случае разводнения.

Базовая и разводненная EPS — наиболее стандартные и часто используемые виды показателя прибыли на одну акцию.

Для более гибкого анализа могут использоваться значение прибыли от продолжающейся деятельности и прибыль без учета чрезвычайных статей.

Прибыль на акцию от продолжающейся деятельности

EPS от продолжающейся деятельности — это прибыль на акцию, которая не включает результаты прекращенной в течение периода деятельности.

Например, компания в течение года закрыла убыточное подразделение. В этом случае инвестору лучше ориентироваться на результат, полученный за счет сегментов, которые и дальше продолжат работу.

Формула расчета разводненной EPS от продолжающейся деятельности выглядит так:

Diluted EPS From Continuing Operations = (NP From Continuing Operations — PD)/ (WACSO + СDS),

NP From Continuing Operations — чистая прибыль компании от продолжающейся деятельности,

PD — сумма дивидендов, выплачиваемая по привилегированным акциям,

WACSO — средневзвешенное количество обыкновенных акций, находящихся в обращении,

СDS — количество акций, которое может добавиться в случае разводнения.

Прибыль на одну акцию за вычетом чрезвычайных статей

EPS без учета чрезвычайных статей — это прибыль на акцию, не учитывающая расходов, которые повлияли на размер прибыли однократно, но обыкновенно не имеют значения для постоянной деятельности компании.

На этот вид прибыли инвестору стоит ориентироваться, если в течение года компания получила прибыль от продажи земли, месторождения и пр.; или, наоборот, если компания получила убыток за счет выплаты штрафов, компенсаций и т. п. То есть в случаях, когда у компании были нехарактерные доходы или расходы.

Формула расчета базовой EPS без учета чрезвычайных статей выглядит так:

Basic EPS Excluding Extraordinary Items = (NP — PD + (-) EI)/WACSO,

NP — чистая прибыль компании,

PD — сумма дивидендов, выплачиваемая по привилегированным акциям,

WACSO — средневзвешенное количество обыкновенных акций, находящихся в обращении,

EI — чрезвычайные статьи расходов или доходов.

Где смотреть показатель EPS

Компании публикуют значение базовой и разводненной прибыли на акцию в одной их основных форм финансовой отчетности — в отчете о прибылях, убытках и прочем совокупном доходе.

Для расчета EPS от продолжающейся деятельности и EPS без учета чрезвычайных статей, если компания сама не опубликовала эти показатели, значения прибыли от продолжающейся деятельности и чрезвычайные статьи доходов и расходов можно также найти в отчете о прибылях, убытках и прочем совокупном доходе или в примечаниях к отчету.

Как инвестор может использовать EPS

Показатель EPS публикуется в самой финансовой отчетности и достаточно удобен для инвестора как в понимании, так и в применении. Использовать его можно в нескольких случаях.

Прибыльность

Положительное значение EPS означает прибыль, отрицательное — убыток. EPS дает возможность неискушенному в отчетности инвестору сравнить прибыль компании с ценой акции. При этом темпы роста EPS дадут инвестору более правильное представление, чем просто темп роста прибыли, поскольку EPS также учитывает изменение количества акций компании. Чем больше значение EPS и чем больше темпы его роста, тем лучше.

Консенсус-прогнозы

EPS — один из основных показателей, прогнозы по которым дают аналитики. Инвестор может ориентироваться на такие прогнозы, чтобы понять, насколько хорошие результаты показала компания по итогам отчетности. Чем лучше EPS в опубликованной отчетности по сравнению с консенсус-прогнозом аналитиков, тем лучше для инвестора.

Мультипликаторы

Для сравнения акций разных компаний важно соотносить EPS со стоимостью акции. Для этого применяется мультипликатор P/E, где P — текущая цена акции, а E — EPS, инвестор может оценить, насколько акция недооценена или переоценена в сравнении с акциями конкурентов. Чем меньше значение P/E при сравнении с акциями схожих компаний, тем более недооценена акция и больший потенциал роста она имеет.

Дивиденды

Если компания платит дивиденды, исходя из размеров полученной прибыли (дивиденды могут выплачиваться, исходя из других показателей — EBITDA , свободный денежный поток ), то размер EPS позволит оценить и размер будущих дивидендов.

Какие у EPS есть недостатки

Как прибыль в целом, так и EPS не учитывают некоторые важные аспекты деятельности компании. Например, уровень долговой нагрузки и размер капитальных вложений. Бывает, что компания с большим EPS даже при сопоставимой цене акций может иметь более значительный размер долга, более высокий уровень капитальных затрат или более низкую рентабельность капитала. То есть инвестору нужно не забывать об использовании других показателей.

Компания может резко и значительно изменять количество акций в обращении. Это может искажать применение показателя.

EPS также не учитывает цену акции, поэтому этот показатель необходимо сопоставлять с ценой акции.

Рекомендуем наш аккаунт в сети «ВКонтакте» — оперативный контент об инвестициях, много видео и полезных лайфхаков

Показатель, указывающий на количество средств, которое компания может выплатить на каждую обыкновенную акцию из чистой прибыли. Существует в нескольких вариантах. Аналитический показатель, указывающий на объем прибыли до вычета расходов по выплате процентов, налогов, износа и амортизации. Несмотря на свою популярность, комиссия по ценным бумагам США (SEC) не считает его частью Общепринятых Принципов Бухгалтерского Учёта (GAAP). Расчетный показатель. Позволяет оценить уровень недооцененности или переоцененности активов рынком. Считается как отношение показателя, содержащего рыночную стоимость актива (капитализация, цена акции, стоимость бизнеса) с отчетным финансовым показателем (выручка, прибыль, EBITDA и др.). Недооцененность или переоцененность актива оценивается при сравнении значения мультипликатора с мультипликаторами конкурентов. Свободный денежный поток. Средства, оставшиеся у компании после уплаты всех операционных расходов. Соотношение капитализации компании к ее чистой прибыли. Популярный показатель для оценки стоимости акций и поиска недооцененных и переоцененных компаний Дивиденды — это часть прибыли или свободного денежного потока (FCF), которую компания выплачивает акционерам. Сумма выплат зависит от дивидендной политики. Там же прописана их периодичность — раз в год, каждое полугодие или квартал. Есть компании, которые не платят дивиденды, а направляют прибыль на развитие бизнеса или просто не имеют возможности из-за слабых результатов. Акции дивидендных компаний чаще всего интересны инвесторам, которые хотят добиться финансовой независимости или обеспечить себе достойный уровень жизни на пенсии. При помощи дивидендов они создают себе источник пассивного дохода. Подробнее

Как рассчитать доходность? Метод Арсагеры

В данном материале рассказывается о том, как правильно рассчитать доходность портфеля ценных бумаг с учетом вводов/выводов (движения денежных средств).

Как рассчитать доходность? На первый взгляд, дать ответ на этот вопрос несложно. Многие знают, что для того чтобы посчитать доходность, необходимо результат инвестиций разделить на сумму вложенных средств и перевести полученное значение в годовые проценты.

Формула расчета доходности (в % годовых), если не происходило вводов/выводов:

D = ((ΔS)/S_нач) * 365/T * 100%, где

• D – искомая доходность;
• ΔS – результат инвестирования в абсолюте;
• S_нач – сумма первоначальных инвестиций;
• T – количество дней в рассматриваемом периоде.

Но задача расчета доходности многократно усложняется в случае, если в течение рассматриваемого периода осуществлялись вводы и/или выводы средств в рамках инвестиционного портфеля. В таком виде она вызывает затруднения даже у опытных специалистов в области инвестиций. Кроме того, не существует идеального способа подсчета доходности в этом случае, поэтому необходимо согласиться (и хорошо их понимать) с определенными допущениями, которые используются в том или ином методе. Мы предлагаем свое решение данной задачи. Сравнение нашего метода с другими известными способами подсчета доходности будет приведено в отдельном материале.

Начнем с определения того, что же такое вводы и выводы денежных средств. Ввод денежных средств – это направление денег на инвестиции. К примеру, Вы приобрели инвестиционные паи фонда или внесли деньги на брокерский счет – все это является вводом средств. Изъятие инвестиционных средств является выводом средств, то есть в рамках наших примеров выводы возникают при погашении инвестиционных паев или выводе денег с брокерского счета.

Зная, что же такое вводы/выводы, рассмотрим конкретную ситуацию, которая поможет понять логику решения задачи по корректному определению доходности с учетом вводов/выводов средств.

1. Некий инвестор приобрел акций на сумму в 1 000 ₽ (S_нач).
2. Через 3 месяца он купил еще акций на 500 ₽ (S_вв).
3. Еще через 4 месяца инвестору срочно понадобились деньги, и он был вынужден продать часть акций на сумму в 300 ₽ (S_выв).
4. Через год после первоначального приобретения стоимость акций составила 1 300 ₽ (S_итог).

В виде графика данную ситуацию можно представить следующим образом:

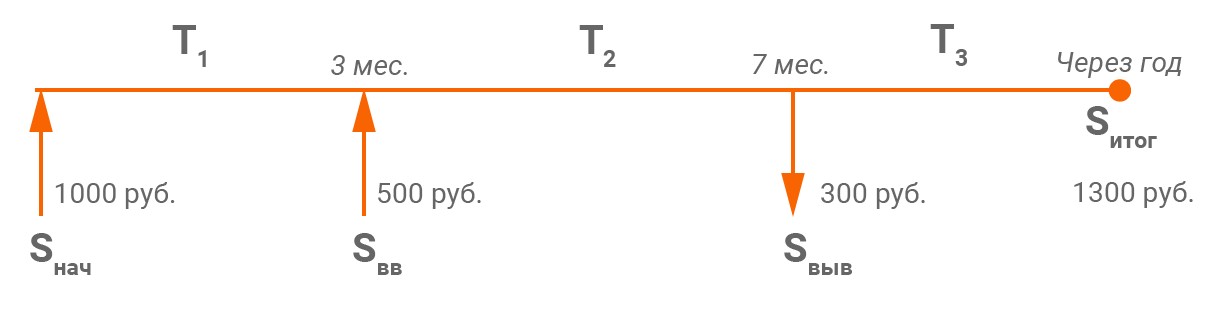
Чтобы корректно рассчитать доходность от инвестиций, нам по-прежнему необходимо разделить результат инвестиций на сумму вложенных средств. Остается только определить, что в рассматриваемой ситуации является результатом и какова корректная сумма вложенных средств.

Первым шагом будет расчет результата инвестиций. И в этом отношении нет никакой сложности, кроме того, финансовый результат вычисляется абсолютно точно. Результат инвестиций – это разница между тем, что мы вывели и имеем на конец периода, и тем, что было вложено. То есть необходимо из суммы стоимости инвестиций на конец периода и всех выводов за период вычесть сумму начального и всех последующих вводов.

Формула для определения результата инвестирования с учетом вводов/выводов:

• ΔS – результат инвестирования за период в абсолюте;
• S_итог – итоговая оценка инвестиций (1 300);
• ΣS_выв – сумма всех выводов средств (300);
• S_нач – сумма первоначальных инвестиций (1 000);
• ΣS_вв – сумма всех вводов средств (500).

Применим данную формулу к рассмотренной ситуации: ΔS = (1 300 + 300) – (1 000 + 500) = 100. Таким образом, инвестор заработал 100 ₽.

Есть любители считать сумму вложенных средств без учета денег, которые были введены на счет (брокерский), но на которые не приобретались ценные бумаги. Такой расчет может резко завысить доходность, хотя прибыль по инвестициям от этого не увеличится. Этот расчет неверен, денежная составляющая инвестиционного портфеля при расчете суммы вложенных средств должна учитываться в полном объеме. Неверно рассчитывать доходность только на часть портфеля, ведь средства, введенные на счет, отвлечены от других целей (потребления, накопления и др.) и являются инвестициями, доходность которых и необходимо узнать.

Второй шаг в расчете доходности является наиболее важным: необходимо корректно определить, с какой суммой соотносить рассчитанный результат инвестирования. А еще точнее, вычислить размер средств в виде единой суммы, которой инвестор как бы оперировал в течение всего периода.

Необходимо согласиться со следующей логикой: в каждый временной подпериод сумма, которой оперировал инвестор, была разной. Начальная сумма была «рабочей» до первого момента ввода или вывода, затем, чтобы понять «рабочую» сумму на следующем подпериоде, её нужно скорректировать на размер ввода (увеличить) или вывода (уменьшить), и так далее для каждого подпериода до конца срока, за который считается доходность.

В подпериод T₁: 1 000 ₽, T₂: (1 000 + 500) ₽, T₃: (1 000 + 500 – 300) ₽. Кроме того, сами по себе эти временные подпериоды не равны. T₁ = 90 дней, T₂ = 120 дней, T₃ = 155 дней. Поэтому необходимо взвесить соответствующую «рабочую» сумму на количество дней в подпериоде, определив таким образом единую средневзвешенную по времени «рабочую» сумму на всем рассматриваемом периоде.

Формула для определения средневзвешенной суммы с учетом вводов/выводов:

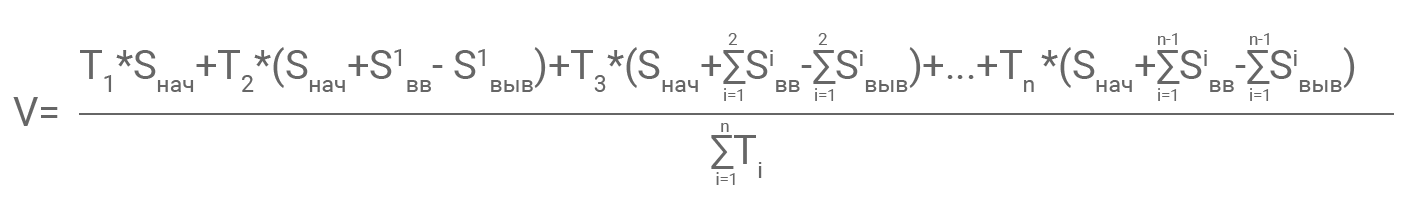
где V – средневзвешенная сумма,

ΣT_i – суммарное количество дней на рассматриваемом временном отрезке.

Применим данную формулу к рассмотренной ситуации:

V = (90 * 1 000 + 120 * (1 000 + 500) + 155 * (1 000 + 500 – 300))/365 = 1 249,32.

Средневзвешенная сумма вложенных инвестором средств составила 1 249,32 ₽.

Теперь известны все элементы, необходимые для непосредственного расчета доходности.

Если Вы хотите рассчитать доходность на периоде, который не включает в себя первоначальный ввод средств, то за S_нач необходимо принять стоимость инвестиционного портфеля на ту дату, с которой Вы хотите начать расчет доходности.

Третий шаг – расчет доходности из полученных значений. Для этого поделим рассчитанный ранее результат инвестирования на средневзвешенную сумму вложенных средств и переведем полученный результат в годовые проценты.

Формула следующая: D = (ΔS/V) * 365/T * 100%

Получается, что в рассмотренной ситуации доходность составляет: (100/1 249,32) * 365/365 * 100% = 8% годовых.

Это аналогично тому, что у инвестора не было никаких вводов/выводов, и он просто в самом начале вложил сумму в размере 1 249,32 ₽, весь период ей оперировал, а в итоге получил прибыль в размере 100 ₽.

Также можно использовать формулу, учитывающую сложный процент:

D = (1 + (ΔS/V)) 365/T – 1

Используя данные формулы, Вы всегда сможете корректно оценить доходность инвестиционного портфеля и при помощи полученных значений оценить эффективность Ваших инвестиций.

Теперь рассмотрим некоторые нестандартные случаи, с которыми можно столкнуться на практике (у нас они случались не раз).

1-й вырожденный случай

Рассмотрим следующий пример:

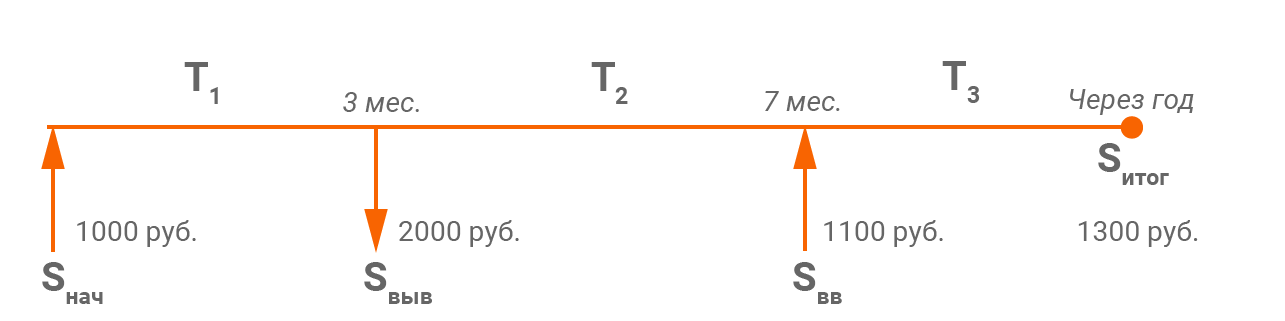
Ввели 1 000 ₽, спустя 3 месяца наши инвестиции утроились (вот такая удача!), что позволило нам вывести 2000 ₽, затем через 7 месяцев мы ввели сумму 1100 ₽, а по окончании года с момента начала инвестиций стоимость нашего портфеля составила 1300 ₽. Таким образом, прибыль за весь срок:

ΔS = (1 300 + 2 000) – (1 000 + 1 100) = 1 200

С оценкой прибыли проблем никаких нет – здесь все корректно, как и произошло на практике.

А вот с расчетом средневзвешенной рабочей суммы возникают сложности. На втором временном отрезке сумма получается отрицательная (– 1 000). Вес ее настолько велик, что и вся средневзвешенная сумма на периоде получается отрицательной.

V = (90 * 1 000 + 120 * (1 000 – 2 000) + 155 * (1 000 – 2 000 + 1 100))/365 = (90 * 1 000 + 120 * (-1 000) + 155 * 100)/365 = –39,73

Корректно оценить размер полученной доходности не получается. Поэтому мы доработали наш метод. В таких случаях, отрицательные суммы, получившиеся на определенных временных отрезках, делаем равными нулю (считаем, что работа ведется заработанной ранее прибылью, то есть нулевой рабочей суммой на этом подпериоде). Как следствие, если:

Таким образом, в данном примере:

V = (90 * 1 000 + 120 * (1 000 – 2 000) + 155 * (1 000 – 2 000 + 1 100))/365 = (90 * 1 000 + 120 * 0 + 155 * 100)/365 = 289,04

D = (ΔS/V) * 365/T * 100% = (1 200/289,04) * 365/365 * 100% = 415,17% годовых.

Или D = (1 + (ΔS/V)) 365/T – 1 = (1+(1 200/289,04)) 365/365 – 1 = 4,1517 или 415,17% годовых.

Данный результат, на наш взгляд, является значительно более правдоподобным.

2-й вырожденный случай

Предположим, Вы осуществляете регулярные инвестиции и в начале каждого квартала в течение 2 лет вносите определенную сумму, например, 1 000 ₽. Таким образом вы внесли 8 000 ₽ за весь период. Несложно посчитать, что средневзвешенная рабочая сумма на этом периоде составит 4 500 ₽.

Например, на рынке случился грандиозный обвал (так было в конце 2008 года), и стоимость Вашего портфеля на конец периода составила 3 000 ₽. Рассчитаем доходность таких инвестиций:

ΔS = 3 000 – 8 000 = – 5 000

Таким образом, отрицательная переоценка больше половины внесенных средств и, что особенно важно, превышает размер средневзвешенной рабочей суммы 5 000 > 4 500. Тогда расчет по формуле:

D = (1 + (ΔS/V)) 365/T – 1, становится не возможен!

D = (1 + (–5 000/4 500)) 365/730 – 1, так как отсутствует математическая возможность вычисления квадратного корня из отрицательного числа.

Действительно, ситуация выглядит несколько абсурдно, так как потери как бы превышают рабочую сумму. При этом, естественно, потери не больше суммы всех внесенных средств.

В таких случаях мы используем исключительно простую формулу доходности:

D = (ΔS/V) * 365/T * 100% = (–5 000/4 500) * 365/730 * 100% = –55,56% годовых.

Она, пусть и при определенных допущениях, но более наглядно оценивает доходность таких инвестиций.

Источник https://www.tinkoff.ru/help/invest/tools/yield-analysis/math-method/

Источник https://quote.rbc.ru/news/article/626ff76a9a794774f6c4613a

Источник https://arsagera.ru/kuda_i_kak_investirovat/kak_invest_sam/kak_rasschitat_dohodnost/